Vector Search... Closest Doesn't Always Mean Similar

The basis of Vector Search (hereinafter referred to as "search") is to find nearby items using various mathematical methods.

However, I suddenly wondered: While nearest neighbor search is clearly correct and mathematically sound, is it truly finding similar articles?

In fact, the search used in durumis finds the six closest articles to a given article in a 768-dimensional space.

But I started to question whether these similar articles are actually similar. (Sometimes, dissimilar articles appear...)

So, what is the reason?

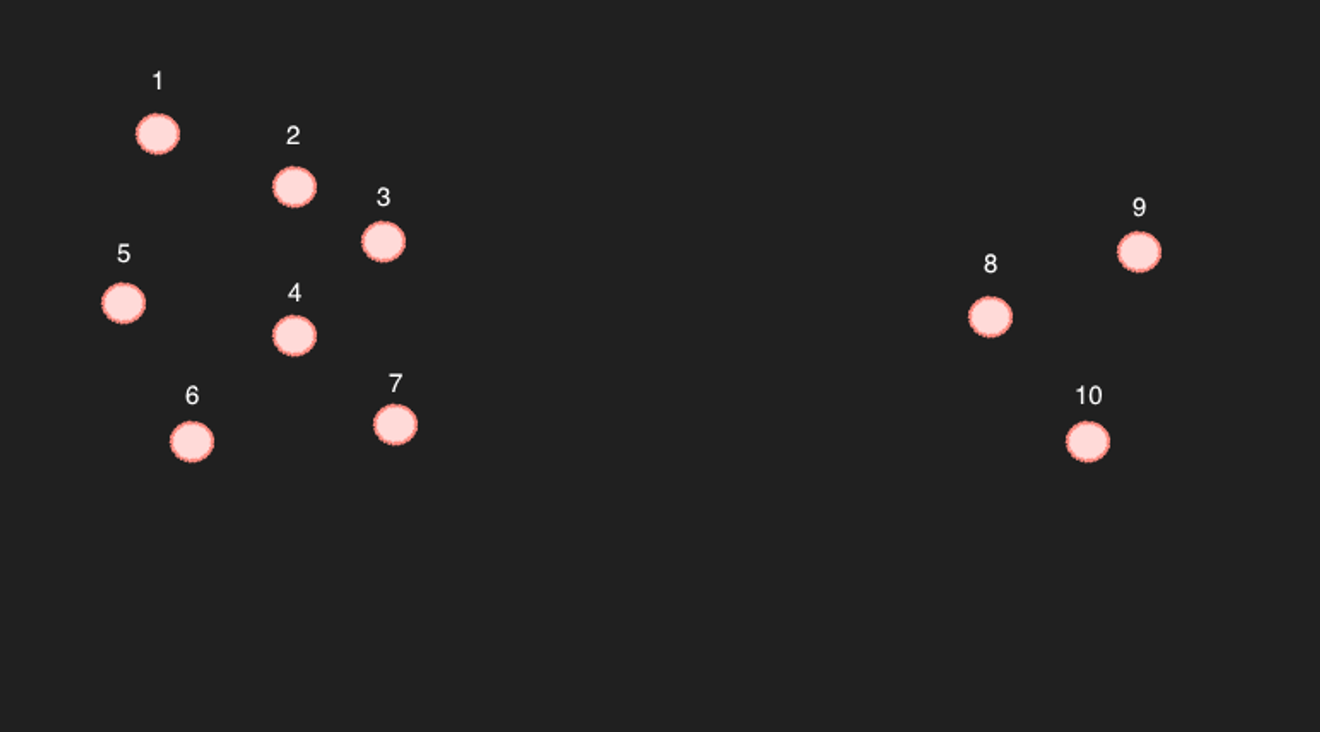
Let's take the example of 10 points in a simplified two-dimensional space.

For points 1 to 7, if you select the six nearest points, the remaining six points will definitely be marked as the closest points. (This is true from a computational standpoint.)

The problem lies with points 8 to 10... For example, if we search for the six closest points to point 9, they would likely be points 8, 10, and 3, 4, 7.

However, this is a problem because, conversely, point 9 is not included among the six closest points to point 4. Are these truly related articles?

The above example is a rather extreme case. If there are sufficiently many points so that there are not such large empty spaces, it might be possible to consider them sufficiently close. (However, considering that it is a 768-dimensional space, there are bound to be empty spaces in between, unless there are a truly vast number of articles...)

I'm still thinking about this, but the most certain solution is that this problem will be resolved if there are enough articles, right?