Temat
- #Przestrzeń o wysokim wymiarze (고차원 공간)
- #Wyszukiwanie podobieństwa (유사도 검색)
- #Rozkład danych (데이터 분포)
- #Wyszukiwanie wektorowe (Vector Search)
- #Wyszukiwanie najbliższego sąsiada (최근접 검색)
Utworzono: 2024-11-23
Utworzono: 2024-11-23 17:13
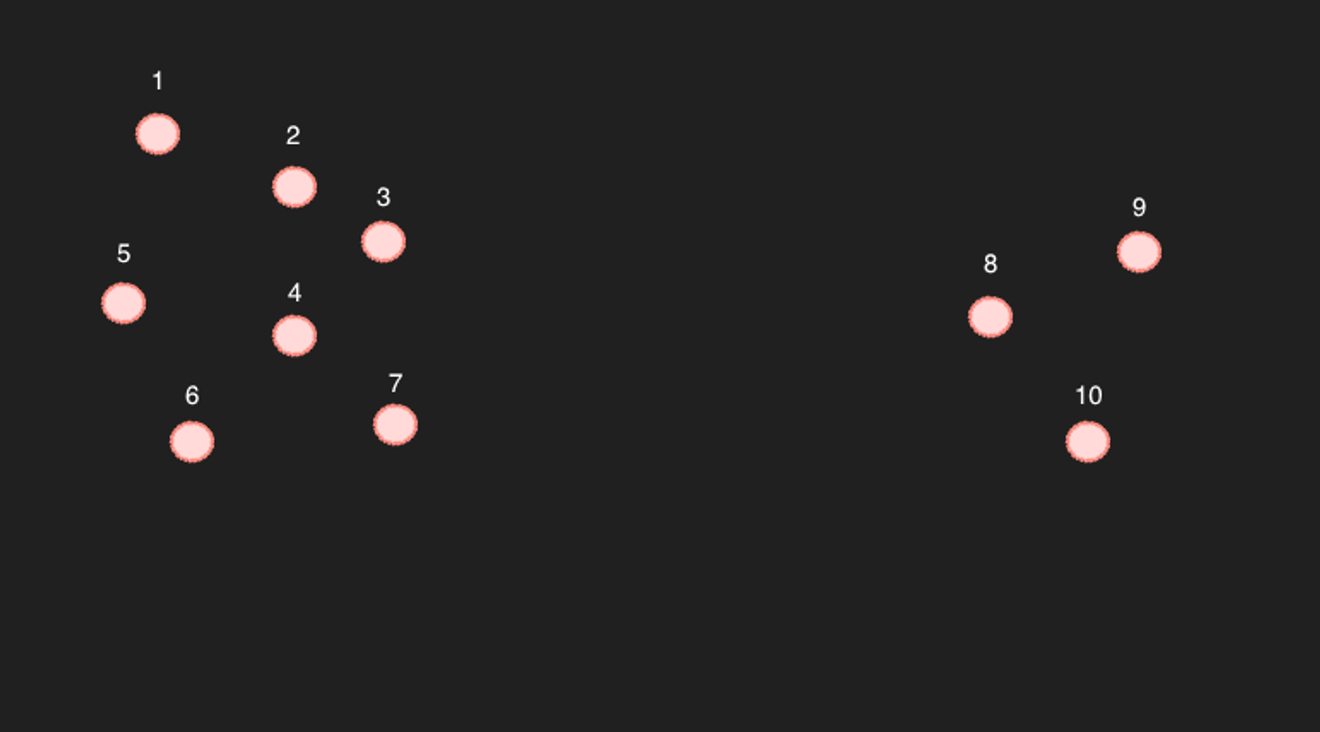
Przykład rozkładu
Podstawą wyszukiwania wektorowego (zwanego dalej wyszukiwaniem) jest znajdowanie obiektów znajdujących się w bliskiej odległości za pomocą różnych metod matematycznych.
Nagle jednak pojawiło się pytanie. Czy wyszukiwanie najbliższego sąsiedztwa jest rzeczywiście poprawne i matematycznie uzasadnione, a jednocześnie zwraca rzeczywiście podobne wpisy?
W wyszukiwaniu używanym w serwisie durumis (두루미스) jeden wpis jest wyszukiwany jako sześć najbliższych wpisów w 768-wymiarowej przestrzeni.
Zastanawiałem się jednak, czy te podobne wpisy są rzeczywiście podobne. (Czasami pojawiają się wpisy, które wcale nie są podobne...)
Jaki jest więc powód?
Weźmy jako przykład 10 punktów w uproszczonej dwuwymiarowej przestrzeni.
W przypadku punktów od 1 do 7, jeśli wybierzemy 6 najbliższych punktów, pozostałe 6 punktów będą z pewnością najbliższymi punktami. (Potwierdzają to obliczenia).
Problem pojawia się w przypadku punktów od 8 do 10... Na przykład, jeśli w wyszukiwaniu znajdziemy 6 najbliższych punktów dla punktu 9, będą to prawdopodobnie punkty 8, 10 oraz 3, 4, 7.
To jednak rodzi problem: odwrotnie, w przypadku punktu 4, punkt 9 nie znajduje się wśród 6 najbliższych punktów. Czy zatem są to rzeczywiście powiązane wpisy?
Powyższy przykład jest dość ekstremalnym przypadkiem. Jeśli jednak istnieje wystarczająco dużo punktów, tak aby przestrzenie między nimi nie były zbyt duże, można uznać je za wystarczająco bliskie. (Jednak biorąc pod uwagę 768 wymiarów, prawdopodobnie będą istniały puste przestrzenie pomiędzy punktami. Przynajmniej jeśli nie ma bardzo dużej ilości wpisów...)
Rozważam to, ale najpewniejszym rozwiązaniem jest zapewnienie wystarczającej ilości wpisów, aby rozwiązać ten problem, prawda?
Komentarze0