Vector Search.. duidelijk dichtbij, maar klopt het wel..

De basis van Vector Search (hierna: zoekopdracht) is het vinden van objecten die dichtbij elkaar liggen, door middel van diverse wiskundige methoden.

Maar toen kreeg ik een vraag. Is de dichtstbijzijnde zoekopdracht, hoewel deze correct en wiskundig juist is, wel echt een vergelijkbaar artikel?

De zoekopdracht die bij durumis wordt gebruikt, zoekt in een 768-dimensionale ruimte naar de zes dichtstbijzijnde artikelen bij een bepaald artikel.

Maar ik begon me af te vragen of vergelijkbare artikelen wel echt vergelijkbaar zijn. (Soms worden er immers artikelen weergegeven die niet vergelijkbaar zijn...)

Wat is dan de reden?

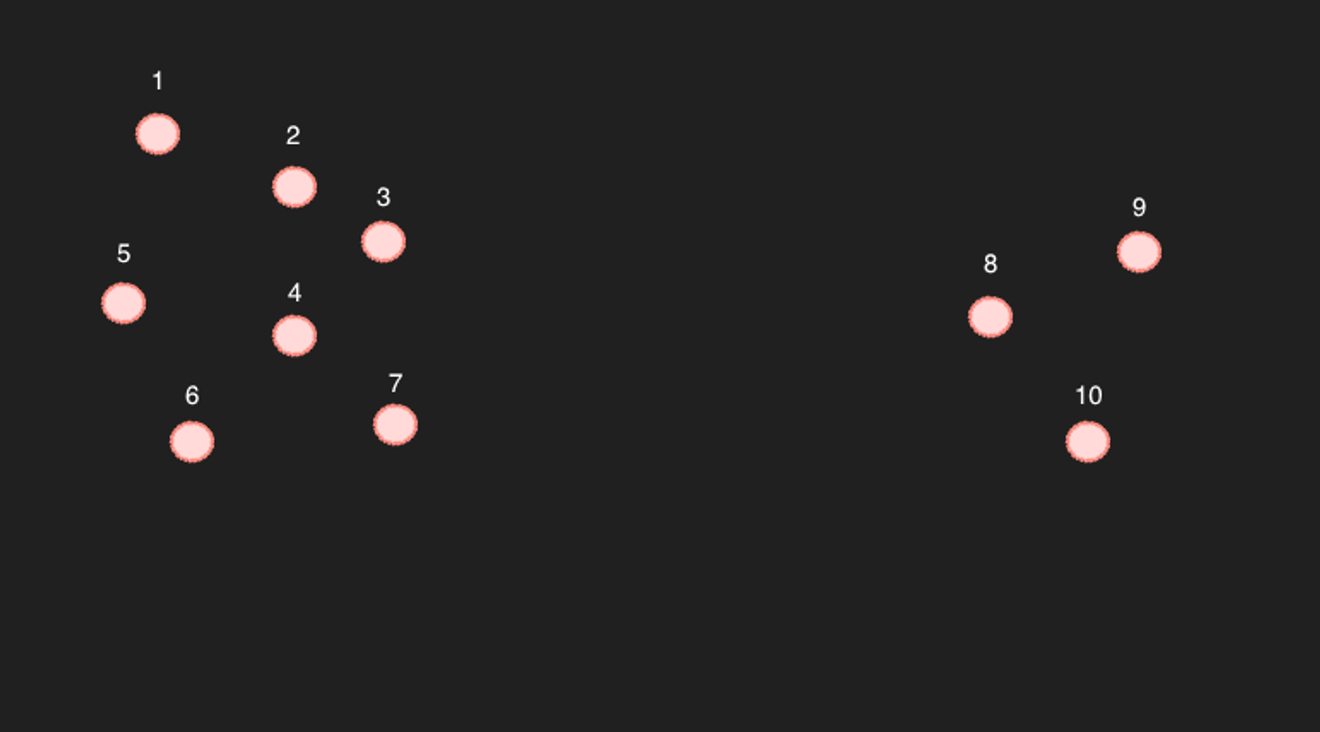
Laten we eens kijken naar het voorbeeld van 10 punten in een vereenvoudigde tweedimensionale ruimte.

Bij punten 1 tot en met 7 is het duidelijk dat als je de 6 dichtstbijzijnde punten selecteert, de overige 6 punten als dichtstbijzijnde punten worden aangegeven. (Dit is ook het geval bij daadwerkelijke berekening)

Het probleem zit hem in punten 8 tot en met 10... Als je bijvoorbeeld de 6 dichtstbijzijnde punten van punt 9 zoekt, dan lijken dat 8, 10 en 3, 4, 7 te zijn.

Maar dat is een probleem, want omgekeerd komt punt 9 niet voor in de 6 dichtstbijzijnde punten van punt 4. Zijn dit dan wel echt gerelateerde artikelen?

Het bovenstaande voorbeeld is een nogal extreem geval. Als er echter voldoende punten zijn zodat er geen grote lege ruimtes zijn, dan zou het wellicht voldoende dichtbij kunnen worden beschouwd. (Maar als je bedenkt dat het om 768 dimensies gaat, zullen er waarschijnlijk toch wel lege ruimtes zijn. Tenzij er heel veel artikelen zijn...)

Ik ben er nog mee bezig, maar de meest voor de hand liggende oplossing is dat dit probleem wordt opgelost als er voldoende artikelen zijn.