Sujet
- #Espace à hautes dimensions
- #Recherche de similarité
- #Recherche vectorielle
- #Recherche du plus proche voisin
- #Distribution des données
Création: 2024-11-23
Création: 2024-11-23 17:13
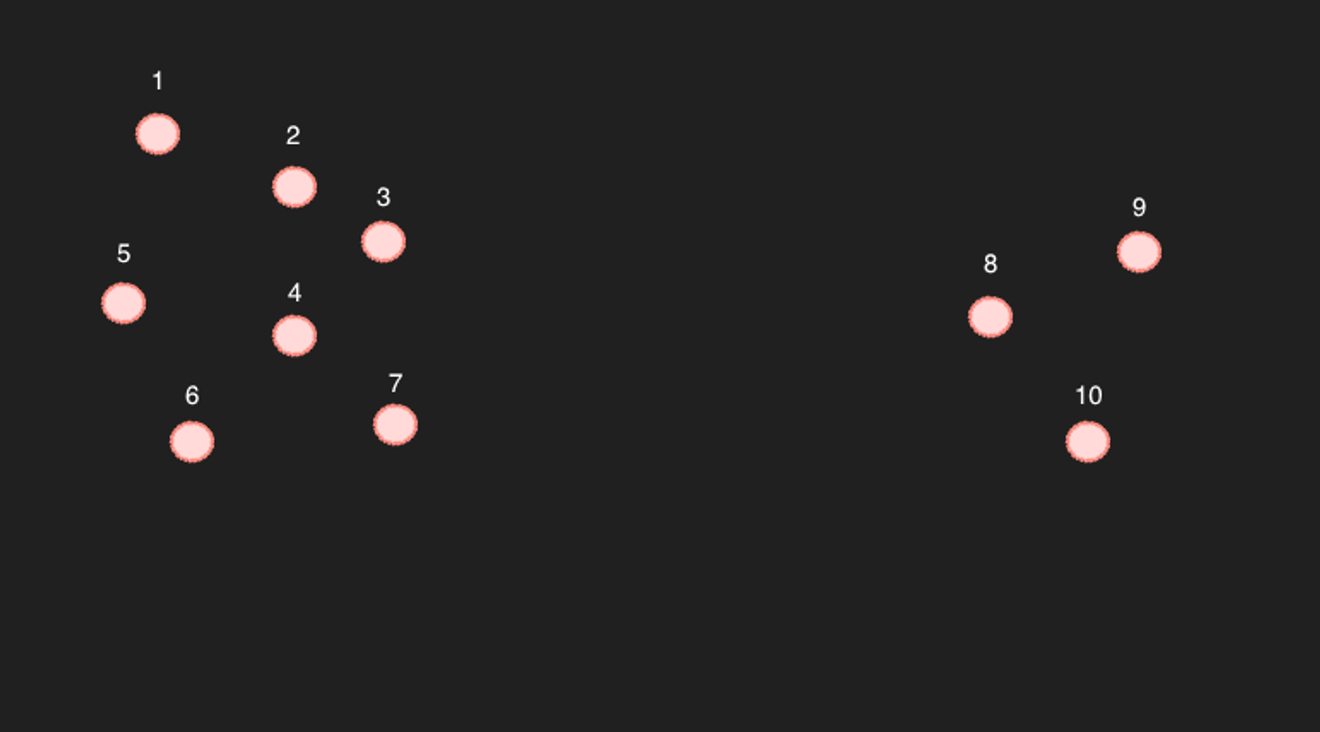
Exemple de dispersion
La base de la recherche vectorielle (ci-après recherche) consiste à trouver les éléments les plus proches à l'aide de diverses méthodes mathématiques.
Cependant, une question m'est venue à l'esprit. La recherche des plus proches voisins est certes exacte et mathématiquement correcte, mais est-ce que cela correspond à des articles similaires ?
En réalité, la recherche utilisée par durumis consiste à rechercher les 6 articles les plus proches d'un article donné dans un espace à 768 dimensions.
Pourtant, je me suis interrogé sur le fait que les articles similaires soient réellement similaires. (parfois, des articles non similaires apparaissent...)
Alors, quelle est la raison ?
Prenons l'exemple de 10 points dans un espace bidimensionnel simplifié ci-dessus.
Pour les points 1 à 7, il est certain que si l'on sélectionne les 6 points les plus proches, les 6 autres points seront indiqués comme les points les plus proches. (c'est le cas en termes de calcul)
Le problème se pose avec les points 8 à 10... Par exemple, si l'on recherche les 6 points les plus proches du point 9, il semble que ce soient les points 8, 10, et 3, 4, 7.
Mais voilà le problème : inversement, le point 9 n'est pas inclus dans les 6 points les plus proches du point 4. Sont-ils vraiment des articles liés ?
L'exemple ci-dessus est un cas assez extrême. Si suffisamment de points sont présents pour que les espaces vides ne soient pas aussi grands, cela pourrait être considéré comme suffisamment proche. (Cependant, compte tenu de la dimension 768, des espaces vides intermédiaires sont inévitables. À moins qu'il n'y ait vraiment beaucoup d'articles...)
Je réfléchis encore à la question, mais la solution la plus sûre est que ce problème sera résolu si suffisamment d'articles sont disponibles, n'est-ce pas ?
Commentaires0