Tema
- #Búsqueda Vectorial
- #Búsqueda de similitud
- #Espacio de alta dimensión
- #Distribución de datos
- #Búsqueda del vecino más cercano
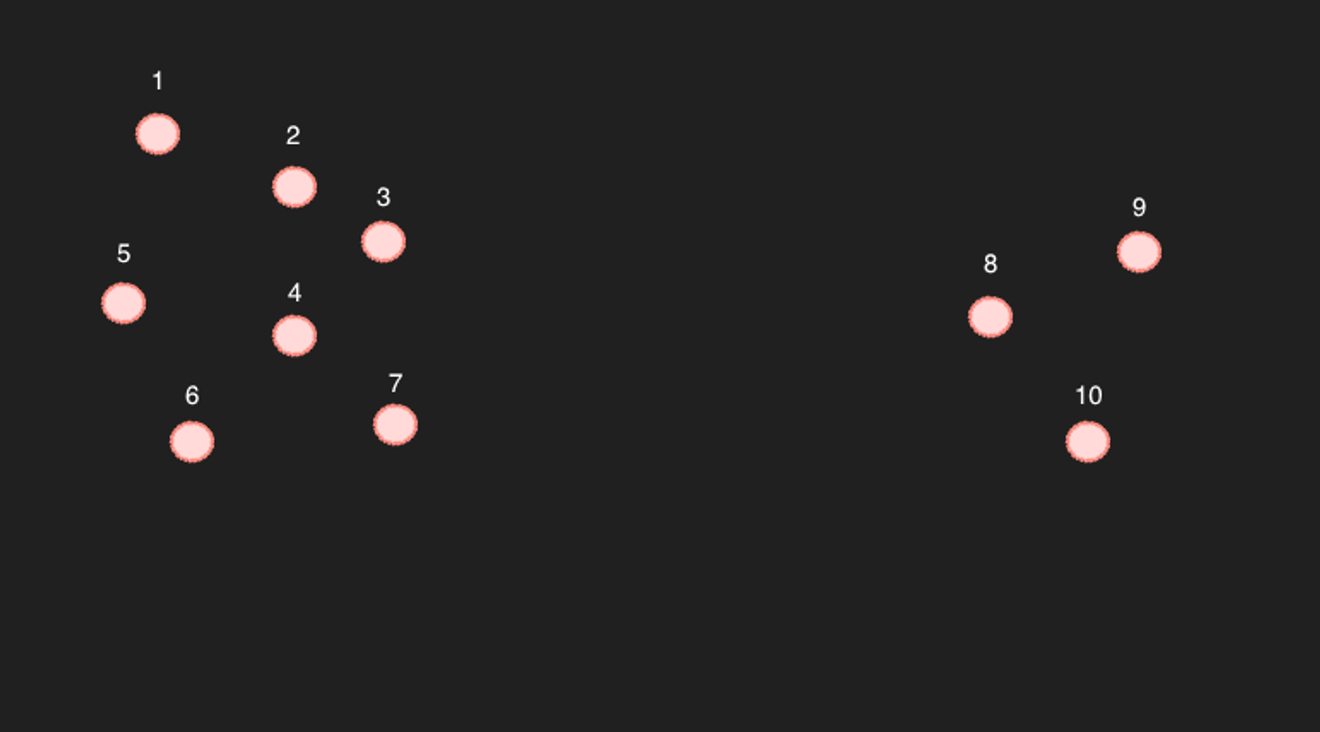
Ejemplo de dispersión
La base de la búsqueda vectorial (en adelante, búsqueda) consiste en encontrar, mediante diversos métodos matemáticos, los elementos que se encuentran a una distancia cercana.
Sin embargo, me surgió una duda. Si bien la búsqueda de los elementos más cercanos es correcta y matemáticamente precisa, ¿se trata realmente de artículos similares?
En realidad, la búsqueda que utiliza durumis (두루미스) consiste en buscar los 6 artículos más cercanos a un artículo dado en un espacio de 768 dimensiones.
Pero comencé a cuestionarme si esos artículos similares lo son realmente. (A veces aparecen artículos que no son similares...)
¿Cuál es entonces la razón?
Tomemos como ejemplo los 10 puntos en un espacio bidimensional simplificado que se muestran arriba.
En el caso de los puntos del 1 al 7, es cierto que al seleccionar los 6 puntos más cercanos, los 6 puntos restantes se muestran como los puntos más cercanos. (Matemáticamente, esto también es cierto).
El problema radica en los puntos del 8 al 10... Por ejemplo, si buscamos los 6 puntos más cercanos al punto 9, parece que serían 8, 10 y 3, 4, 7.
Pero aquí surge un problema: a la inversa, el punto 9 no está incluido entre los 6 puntos más cercanos al punto 4. ¿Son realmente artículos relacionados?
El ejemplo anterior es un caso bastante extremo. Si hubiera suficientes puntos para que no hubiera espacios vacíos tan grandes, probablemente se podría considerar que están suficientemente cerca. (Sin embargo, considerando que se trata de 768 dimensiones, es inevitable que existan espacios vacíos intermedios. A menos que haya una gran cantidad de artículos...)
Estoy reflexionando sobre esto, pero la forma más segura de resolver este problema es que haya suficientes artículos, ¿verdad?
Comentarios0