Thema
- #Datenverteilung
- #Vektorsuche
- #Ähnlichkeitssuche
- #Hochdimensionaler Raum
- #Nearest-Neighbor-Suche
Erstellt: 2024-11-23
Erstellt: 2024-11-23 17:13
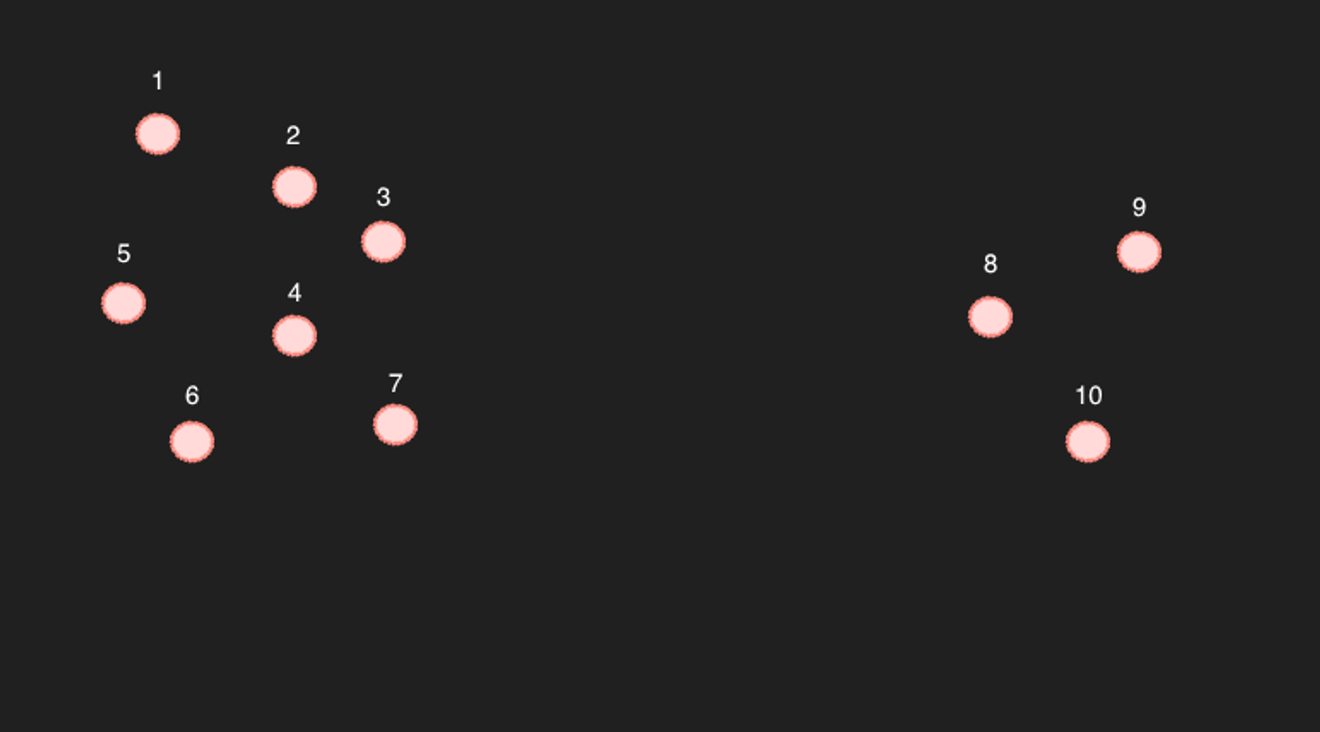
Beispiel der Streuung
Die Grundlage der Vektorsuche (im Folgenden Suche) besteht darin, nahe beieinander liegende Elemente mithilfe verschiedener mathematischer Methoden zu finden.
Doch dann stellte sich mir eine Frage: Die nächste Nachbarsuche ist zwar korrekt und mathematisch richtig, aber ist sie auch wirklich relevant für ähnliche Beiträge?
Die von durumis (두루미스) verwendete Suche findet in einem 768-dimensionalen Raum die sechs nächstgelegenen Beiträge zu einem gegebenen Beitrag.
Ich begann jedoch zu zweifeln, ob die gefundenen ähnlichen Beiträge tatsächlich ähnlich sind. (Manchmal werden auch unähnliche Beiträge angezeigt...)
Worin liegt also der Grund?
Betrachten wir als Beispiel zehn Punkte in einem vereinfachten zweidimensionalen Raum.
Bei den Punkten 1 bis 7 ist es sicher, dass bei Auswahl der sechs nächstgelegenen Punkte die restlichen sechs Punkte als die nächstgelegenen Punkte angezeigt werden. (Das ergibt sich auch aus den tatsächlichen Berechnungen.)
Das Problem liegt bei den Punkten 8 bis 10. Wenn man beispielsweise die sechs nächstgelegenen Punkte zu Punkt 9 sucht, wären dies wahrscheinlich 8, 10 und 3, 4, 7.
Das ist jedoch problematisch. Umgekehrt ist Punkt 9 nicht unter den sechs nächstgelegenen Punkten von Punkt 4 enthalten. Sind dies dann wirklich verwandte Beiträge?
Das obige Beispiel ist ein ziemlich extremes Szenario. Wenn genügend Punkte vorhanden sind, so dass es keine großen leeren Bereiche gibt, könnte man die Punkte als ausreichend nahe beieinander liegend betrachten. (Bei 768 Dimensionen ist es jedoch wahrscheinlich, dass zwischen den Punkten leere Bereiche existieren, es sei denn, es gibt sehr viele Beiträge.)
Ich überlege noch, aber die sicherste Lösung ist wohl, dass dieses Problem behoben wird, wenn genügend Beiträge vorhanden sind.
Kommentare0